Have you ever wondered how a neural network learns to understand complex things like language or images? A big part of the answer lies in a component that acts like a tiny decision-maker inside the network. This component is the activation function, and it is a critical element that significantly impacts the performance of deep neural networks.
Understanding these functions is key to grasping how a network goes from seeing random data to recognizing sophisticated patterns. So, let’s explore what they are, why they are so essential, and how they have evolved.
1. The Core Idea: What Are Activation Functions and Why Do We Need Them?
1.1. What is an Activation Function?
So, what exactly is an activation function?
Imagine a single neuron in a vast network. It receives signals from many other neurons. The activation function acts as a gatekeeper or a switch for this neuron. It takes the combined input signal and decides two things:
- Should the neuron “fire” (pass on a signal) or remain silent?
- If it fires, how strong should that signal be?
In essence, it gives the network the power to create its own “on and off” nodes, which helps it find patterns in the data it processes.
1.2. Why Non-Linearity is Crucial
Okay, but why is this ‘gatekeeper’ so important? Why can’t we just pass the signal along?
The most critical role of an activation function is to introduce non-linearity into the network. Here’s why that matters:
- A neuron without an activation function is just a linear operation (like output = weight * input + bias).
- If you stack many layers of these linear neurons on top of each other, the entire network just collapses back into a single, simple linear equation. You could achieve the same result with just one layer.
- The real world is full of complex, non-linear patterns (think about the shape of a cat in a photo or the grammatical structure of a sentence). A purely linear model is too simple to capture this complexity.
It is the non-linear activation function that allows a deep network to learn and map the complex, non-linear functions found in real-world data.
This need for non-linearity led researchers to early candidates like Sigmoid and Tanh. However, these pioneers faced a major challenge that stalled progress in deep learning for years.
2. The Early Days: The Vanishing Gradient Problem
The first widely used activation functions were Sigmoid and Tanh. They are smooth, non-linear functions that were foundational to early neural networks.
If these functions worked, why did we need new ones?
As networks got deeper (with more layers), they ran into a crippling issue called the “vanishing gradient” problem.
- Analogy: Imagine whispering a message down a long line of people. With each person, the message gets a little quieter and less distinct. By the time it reaches the end of the line, the original message is completely lost.
- In a Network: The “gradient” is the learning signal that gets passed backward through the network during training. With Sigmoid and Tanh, the derivative (or the rate of change) is a number between 0 and 1. When you multiply these small numbers together across many layers, the signal shrinks exponentially.
- The Result: The layers at the beginning of the network receive an almost zero gradient signal, which means they effectively stop learning. This made it incredibly difficult to train deep networks.
This roadblock demanded a new solution—something simple, yet powerful enough to keep the learning signal alive. That solution would spark a revolution in deep learning.
3. The ReLU Revolution: A Simple and Powerful Fix
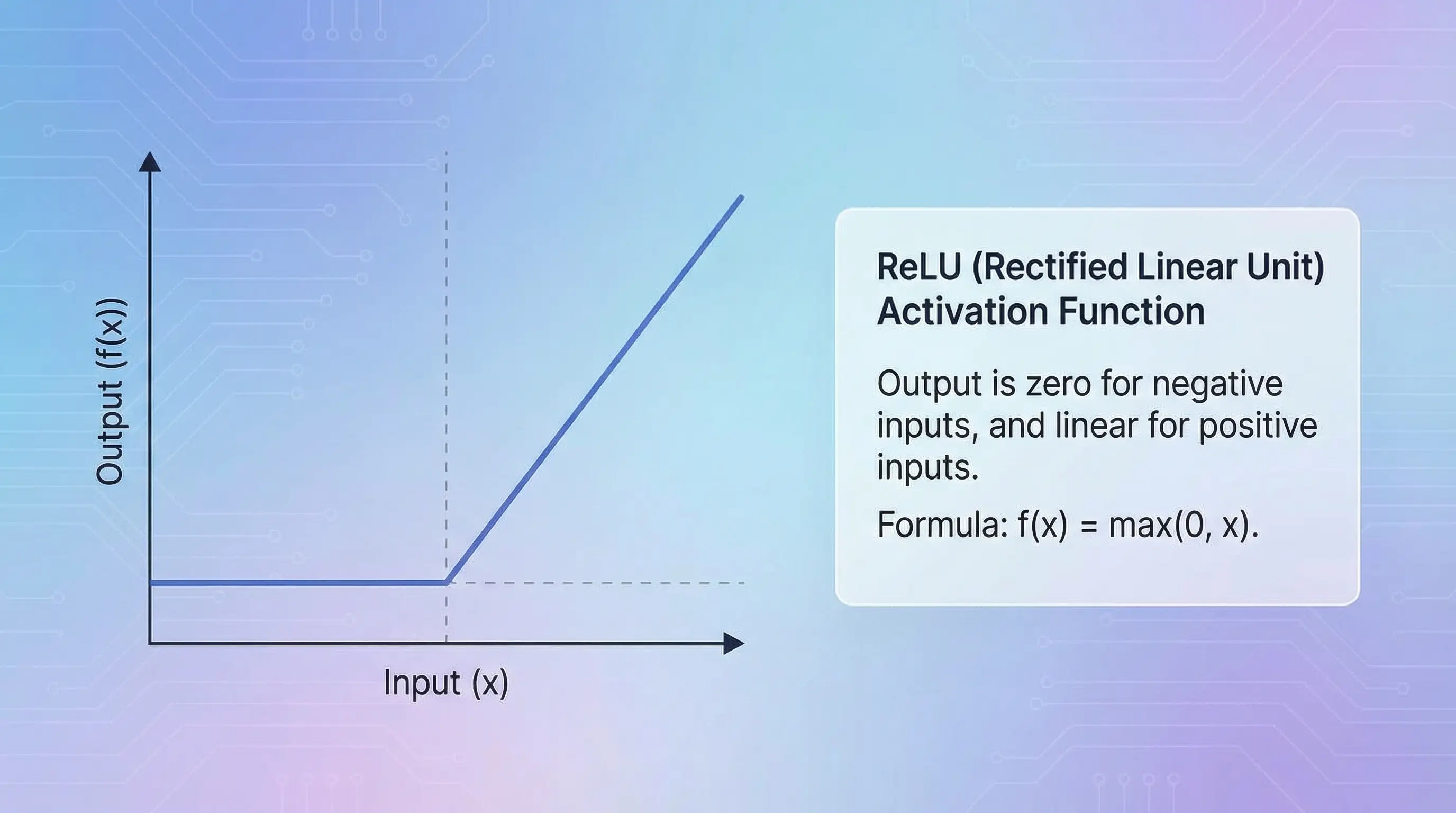
ReLU Activation
3.1. Introducing ReLU (Rectified Linear Unit)
How did researchers solve the vanishing gradient problem?
The answer was a brilliantly simple function called ReLU (Rectified Linear Unit). Its formula is just max(0, x).
Its mechanism is incredibly straightforward:
- If the input (x) is positive, it passes it on unchanged.
- If the input is negative, it outputs zero.
Think of it as the purest form of an “on-off” switch. It either lets the positive signal through or shuts the negative signal down completely.
3.2. ReLU’s Strengths and Weaknesses
ReLU’s simplicity was its greatest strength, but it also came with a significant drawback.
| Pros 👍 | Cons 👎 |
|---|---|
| Solves Vanishing Gradients: For positive inputs, the derivative is a constant 1, so the signal doesn’t weaken across deep layers. Computationally Fast: The max(0, x) operation is extremely efficient. |
The “Dying ReLU” Problem: If a neuron’s inputs are consistently negative, it will always output zero. Its gradient will also be zero, meaning it effectively “dies” and stops learning. |
While ReLU remains a strong and popular choice, the “dying ReLU” problem prompted researchers to develop smoother and more sophisticated functions.
4. The Next Generation: GELU and Swish
How can we get the benefits of ReLU without the ‘dying neuron’ problem?
The next wave of activation functions focused on creating smooth curves that didn’t completely kill negative inputs, allowing for more stable and robust learning.
GeLU Activation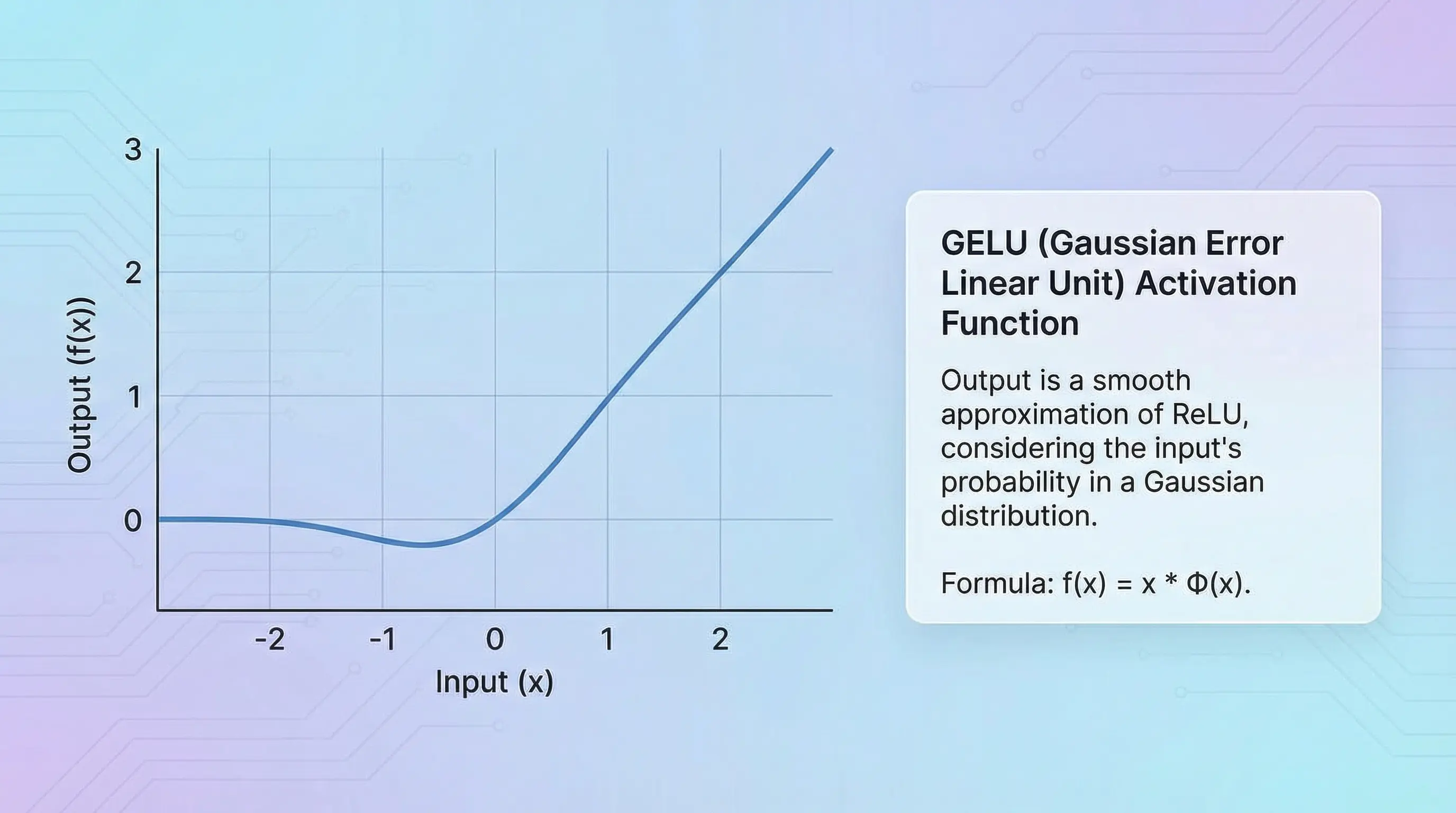
-
GELU (Gaussian Error Linear Unit): GELU is a smoother version of ReLU. Instead of just zeroing out negative inputs, it gently reduces them. The motivation behind GELU was to combine ideas from dropout (a regularization technique) and activation functions. It became popular after being used in landmark models like BERT and GPT-2.
-
Swish (also known as SiLU): Swish is another smooth alternative to ReLU. Its formula is
x * sigmoid(x), which means it uses a sigmoid function to create a “gate” that controls how much of the original input x passes through. This “self-gating” allows for more complex behavior than ReLU.
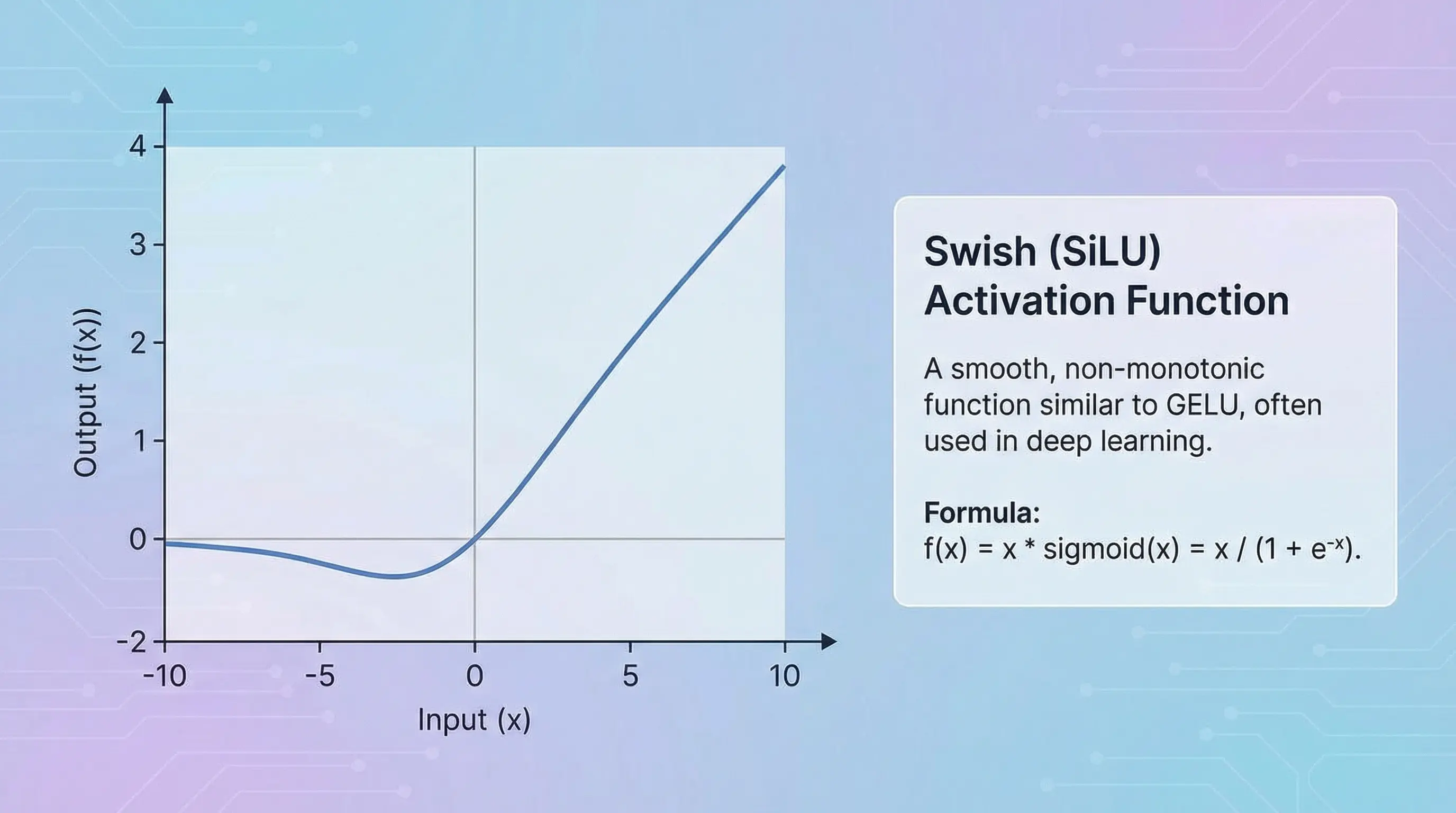
SiLU Activation
Here is a simple comparison of how these functions behave:
| Function Name | How It Handles Negative Inputs | Key Idea |
|---|---|---|
| ReLU | Zeros them out completely. | A simple “on-off” switch. |
| GELU | Gently reduces them, allowing some signal. | A smooth, probabilistic switch. |
| Swish (SiLU) | Can become slightly negative before returning to zero. | A self-gated switch. |
These refinements marked a clear improvement. However, the most powerful models today have moved on to an even more advanced technique based on explicit gating.
5. The State of the Art: GLU Variants in Modern LLMs
5.1. The Gating Idea: More than Just an Activation
What do cutting-edge models like LLaMA and PaLM use?
They use variants of the Gated Linear Unit (GLU). GLU isn’t just a single function; it’s a mechanism. Unlike single-path functions like ReLU or GELU that simply decide to dampen or pass through a signal, the GLU mechanism splits the input into two paths. One path acts as a dynamic, context-dependent filter (the “gate”) that controls how much information from the main path gets through. This added “control knob” gives the Transformer’s feed-forward layer significantly more expressive power.
The formula for this mechanism is: Activation(xW) ⊗ (xV)
Here, one projection of the input (xW) is passed through an activation like Swish or GELU to form the gate, which then controls how much of the information from the other projection (xV) is allowed to pass through via element-wise multiplication (⊗).
5.2. SwiGLU and GEGLU: The New Champions
The top-performing activation functions in modern Transformers are SwiGLU and GEGLU. They are simply GLU variants that replace the original sigmoid gate with the more powerful Swish and GELU functions, respectively.
This gating mechanism gives the network more expressive power to control the flow of information, leading to significant performance improvements in models like Transformers. Even the researchers who discovered their effectiveness were humorously humble about why they work so well, writing in their paper:
“We offer no explanation as to why these architectures seem to work; we attribute their success, as all else, to divine benevolence.”
Today, these functions are at the heart of the world’s most advanced large language models.
- SwiGLU: Used in models like LLaMA (Meta) and PaLM (Google).
- GEGLU: Used in models like Gemma (Google).
This journey—from simple switches to sophisticated, dynamic gates—shows just how much this “secret sauce” has evolved.
6. Conclusion: The Evolutionary Path
The choice of activation function is a critical design decision that has evolved dramatically. We’ve moved from simple functions that introduce non-linearity to complex gating mechanisms that give networks fine-grained control over information flow.
This evolutionary path can be summarized in a table:
| Generation | Key Functions | Core Problem Addressed |
|---|---|---|
| Early Days | Sigmoid, Tanh | Introducing non-linearity |
| The Revolution | ReLU | Vanishing Gradients |
| The Refinements | GELU, Swish | “Dying ReLU” & Smoothness |
| Modern Era | SwiGLU, GEGLU | Improving Transformer performance via gating |
While ReLU remains a strong and simple baseline, the success of GLU variants in today’s largest models shows that this is still an exciting and active area of research in artificial intelligence.
